Where the techniques of Maths
are explained in simple terms.
Calculus - Differentiation - Differentiability.
- Algebra & Number
- Calculus
- Financial Maths
- Functions & Quadratics
- Geometry
- Measurement
- Networks & Graphs
- Probability & Statistics
- Trigonometry
- Maths & beyond
- Index
As we have emphasised on various pages and videos in this website, differentiation is all about gradients. So differentiability is all about determining whether or not we can calculate the gradient of a given curve at all points along the curve.
Discontinuity and differentiability
If a curve is continuous at a point, that means that we can trace the curve with our finger and not lift our finger off the paper.
If however we do lift our finger, then the curve is discontinuous and so we cannot determine its gradient at that point.
A curve cannot be differentiable at a point of discontinuity although it could be differentiable at all other points depending on its definition.
Testing for differentiability
In an concept analogous to that of continuity, a curve is said to be differentiable if the gradient at a given point:
- can be determined; and
- is the limit of the gradient on either side of that point as we move along the curve towards the given point.
Remember that a derivative measures the rate of change at a given point (or at a given time or place).
So to conclude that a curve is differentiable is really saying that the rate of change is smooth and continuous at that point.
Most curves which are continuous at a given point are also differentiable at that point. The gradient is therefore the same on either side or the values are changing smoothly.
For example, the graph of
|
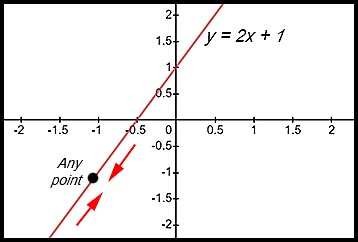 |
For this graph of
|
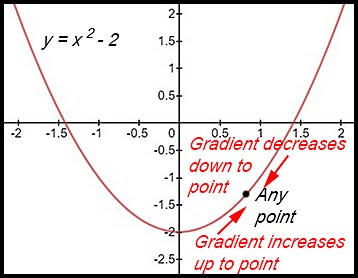 |
For the graph If the domain is restricted to one side of the |
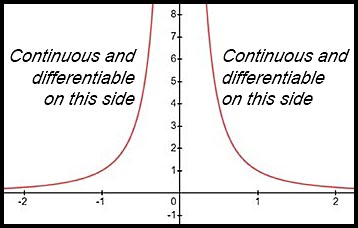 |
The function y = |3x| is continuous. The gradient for x < 0 is negative and the gradient for x > 0 is positive. The gradient at x = 0 cannot be determined and does not follow from the lines on either side. Hence the function is not differentiable at x = 0. |
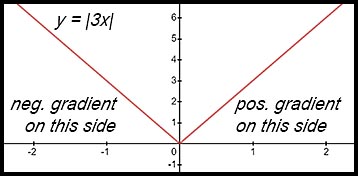 |
No formal proof of differentiability is needed but you need to be able:
- to look at a graph and conclude about its differentiability.
- interpret a point of differentiability as being where the instantaneous change of values does not follow from the changes on either side of the point.
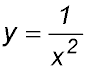 , the curve is discontinuous at x = 0. It therefore is
, the curve is discontinuous at x = 0. It therefore is